| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© snoclub.fr.st
I - LES MODELES ATOMIQUES ANCIENS EN MECANIQUE CLASSIQUE
:
Depuis longtemps, on essaie de modéliser l’atome : on ne peut pas lui appliquer les lois de la mécanique classique. On utilise alors une nouvelle théorie appelée Mécanique Quantique, basée sur la probabilité de présence de l’électron et non plus sur une position bien précise.
1) Le modèle de Rutherford (1911):
Il assimile l’atome à un système planétaire : 2 forces s’appliquent sur un électron :
-La force d’attraction par le noyau
F = ((4pe0)-1 ´ (qq’/r²))
-Et la force centrifuge, colinéaire, de même force, mais opposée à la
première :
Fc = - F
Or Fc = (mv²) / r
Donc : ![]()
(mv²) / r = ((4pe0)-1 ´ (qq’/r²)) Û (1/2)mv² = ((4pe0)-1 ´ (qq’/2r))
Ce qui correspond à L’énergie cinétique de l’électron.
D’après Rutherford, l’énergie cinétique de l’électron dépend de r. L’expérience montre que c’est faux. (L’énergie cinétique de l’électron ne peut prendre que des valeurs distinctes précises : on parle de valeurs discrètes.) Le modèle de Rutherford est donc faux.
2) Contradictions :
a-Relation de DeBroglie
(1924) :
Toute
particule en mouvement est associée à une longueur d’onde :
![]()
l = longueur d’onde h = constante de Planck
m = masse de la particule v = vitesse de l’électron
Selon
DeBroglie, si l’électron émet une
longueur d’onde, il perd
de l’énergie. A terme, l’électron
n’aurait donc plus d’énergie et s’écraserait sur le noyau,
ce qui est faux.
Pour expliquer l’énergie des électrons, on les fait réagir à la lumière, les échanges d’énergie se font par des absorptions et d’un rayonnement spécifique à l’électron.
b-Dualité « nature ondulatoire-corpusculaire » de
la lumière :
Nature ondulatoire :
Un rayonnement a un
caractère ondulatoire (expérience de diffraction / interférence )
La lumière est donc une onde électromagnétique. Son rayonnement (l), s’écrit
l = cT
c = célérité de la lumière (en m/s).
T = durée (en s).
l = rayonnement = longueur d’onde (en m).
Le nombre d’onde (g) est l’inverse de la longueur d’onde :
g = l-1
c-Les spectres de l’atome d’hydrogène :
Il peut y avoir échange d’énergie entre la matière et les rayonnements (photons) dans les deux sens.
Exemple : émission de rayonnement
(par une flamme), absorption de rayonnement (par un corps coloré opaque, qui chauffe quand il est foncé).
Un rayonnement comportant toutes les longueurs d’onde, présente un spectre continu.
Sinon, il présente un spectre discontinu.
L’électron peut être excité avec de la lumière, et peut émettre un rayonnement discontinu.
(Expérience d’un bac à hydrogène excité, puis désexcité, le rayonnement est émis, séparé par un prisme, et on obtient sur un écran quelques bandes blanches : c’est le spectre de l’hydrogène)
Relation de Balmer :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On peut remarquer
sur ce spectre qu’il y a 5 séries de bandes, elles ont toutes un
nom :
- Série de Lyman : ( ultraviolet : l = 100 nm)
- Série de Balmer : (visible : l = 400-600 nm)
- Série de Paschen : (infrarouge proche : l = 1000 nm)
- Série de Brackett : (infrarouge : l = 2000-4000 nm)
- Série de Pfund : (infrarouge lointain : l > 7000 nm)
Chaque série a 2 raies limites( la raie de tête et la raie limite)
![]()
RH est la constante de Rydberg = 1,097 ´ 107 m-1,
z est le numéro atomique (pour l’hydrogène z = 1, donc négligeable.),
l est une longueur d’onde (la distance d’un trait par rapport au 0),
n1 et n2 correspondent à des niveaux d’énergie de l’électron, ces niveaux tabulent. (i.e. L’électron passe brusquement d’un niveau à un autre sans avoir d’étapes intermédiaires).
On peut calculer les différentes énergies de l’électron avec la relation :
Eélectron = -Ephoton = (hc)/l
L’énergie
de l’électron est toujours négative, celle du photon est toujours
positive.
Astuce : pour connaître l’énergie de l’électron sans la comparer à une autre, on prend :
n2 = + ¥ Donc, (n2)-2
= 1/(n2)2 = 0
On parle d’état fondamental de l’atome lorsque l’on est dans le cas de la plus basse énergie (pour l’atome d’hydrogène, quand n=1, E = -13,6 eV)
Lorsque n>1, l’énergie de l’électron a augmenté, l’atome est dans un état excité.
Le passage d’un niveau d’énergie à un autre est appelé transition. L’état excité est instable, l’atome tend vers état fondamental (et émet un rayonnement comme dans l’expérience du prisme plus haut), c’est la transition inverse.
Explication des raies et des séries:
La première série
(Lyman) correspond à une transition de n=1. Les raies dans la série
correspondent à la destination de la transition. Ainsi, une transition
de l’état n=3 à n=5 sera représentée par le 5è trait de la 3è série
(Paschen). En mesurant la longueur d’onde ainsi obtenue, on
pourra calculer facilement avec la relation de dessus l’énergie qui
a été nécessaire à cette transition.
d-Le spectre d’absorption de l’hydrogène.
Prenons la même expérience avec le prisme : On éclaire l’hydrogène avec un spectre continu, et on obtient un spectre discontinu : l’hydrogène est excité (il a absorbé des radiations).
C’est exactement l’inverse que dans le cas de l’émission, avec les mêmes formules, mais l’énergie d’un photon est positive, les longueurs d’ondes sont toujours positives.
3) Le modèle de BOHR SOMMERFIELD :
On a essayé de modifier le principe de Rutherford pour qu’il devienne juste.
Bohr et Sommerfield ont gardé le principe de la mécanique classique mais en ajoutant 2 postulats :
* Les électrons restent
sur des orbites privilégiées : orbites
stationnaires. Ils n’émettent pas
de rayonnements et ne perdent donc pas d’énergie.
* L’électron peut passer d’une
orbite stationnaire à une autre si le milieu extérieur lui fourni de l’énergie
sous forme discontinue, c’est la « tabulation ». Le périmètre de l’orbite (assimilée à un cercle) se
calcule avec la formule
2pr = nl
n est un entier naturel. D’après le principe de Debreuil :
![]()
mvr est appelé « moment cinétique orbitale »
On peut alors calculer la vitesse de l’électron autour du noyau en fonction de r .
On sait que la somme des forces extérieures (premier membre) est le produit de la masse (m) et de l’accélération (a = v2/r, ici centripète). Donc,
![]()
et en se servant de l’égalité de la vitesse de Debreuil, on a :
![]()
On voit donc bien que le rayon (r) et la vitesse ne peuvent prendre que des valeurs distinctes puisque n est un naturel : n est appelé nombre quantique principal.
En se servant de l’énergie cinétique de l’électron (voir Rutherford), on trouve que :

C’est l’énergie totale de l’atome d’hydrogène ( à 1 électron), elle ne dépend que de n. C’est ainsi que l’on peut trouver que son énergie est de 13,6 eV quand n=1 (niveau fondamentale).
Le rayon de l’atome de BOHR (qui
est le rayon r quand n=1) est de 0,053 nm
= 1 ula
Pour les hydrogénoïdes avec z ¹ 0 et 1 électron, on a bien un z plus grand, donc les longueurs d’onde seront plus petites, donc le spectre sera plus dur à observer.
Exemple : calculons les 5 premiers niveaux d’énergie de l’hydrogénoïde
avec 1 électron et z=2 :
En = (-13, 6 ´ z²)/n² (après
on remplace n par 1, 2, 3, 4, 5)
II - MODELE ATOMIQUE EN MECANIQUE ONDULATOIRE.
Le modèle de BOHR ne marche que lorsqu’il n’y a qu’un seul électron. On doit donc considérer que l’électron a un double aspect : corpusculaire et ondulatoire. Ce double aspect est à l’origine de la mécanique quantique.
1) Le modèle d’ Heisenberg :
Il est impossible de mesurer la trajectoire exacte des électrons sans perturber leur course, d’où le principe d’Heisenberg: l’incertitude.
Mis en équation, cela donne : ![]() . Tout ceci est le produit des incertitudes de la position et
de la vitesse. Ceci est valable
aussi bien pour un électron que pour un mastodonte, cependant l’onde
associée a une masse importante n’a aucune signification, elle en
a pour une petite masse.
. Tout ceci est le produit des incertitudes de la position et
de la vitesse. Ceci est valable
aussi bien pour un électron que pour un mastodonte, cependant l’onde
associée a une masse importante n’a aucune signification, elle en
a pour une petite masse.
Ce principe donne une délimitation entre l’aspect corpusculaire et l’aspect ondulatoire.
Exemple1 :Une voiture a une masse de 1tonne, une vitesse de 100 km/h
à n1<n2 km/h d’incertitude. On applique
la relation et on trouve une incertitude sur la position de 3,8´10-34m. Ceci n’a donc aucune signification.
Exemple 2 : Un atome H a une incertitude sur sa vitesse de 1 cm/s . Sa
masse est de 1 uma. L’incertitude sur sa position est de 6300 nm.
Exemple 3 : un électron : incertitude sur la vitesse de 100 m /s, donc l’incertitude sur sa position est de 11,5 µm.
La mécanique quantique est une théorie qui va permettre de déterminer précisément les énergies possibles de l’électron, on ne va plus se soucier de sa trajectoire exacte, on va se soucier de connaître la probabilité de trouver l’électron en un point donné de l’espace, et cela repose sur la nature ondulatoire de l’électron.
A cet électron on associe une fonction d’onde :
Définition :
Le propagation d’une onde due à un électron est étudiée à partir de son amplitude. On représente cette amplitude par la fonction :
y(x,y,z,t) = y(x,y,z) ƒ(t) p
Pour un électron à l’état fondamental, sa durée de vie est infinie, son amplitude est donc constante en un point donné quelque soit le temps. On dit alors que l’onde est stationnaire et f(t) est donc une constante.
La fonction d’onde est calculée à partir de l’équation dite de SCHROEDINGER.
H(y) = E(y)
H est un opérateur, « le Hamilton », et E est l’énergie de l’électron.
La résolution de cette équation donne donc des couples : l’énergie et la fonction d’onde associée. Cette équation permet de calculer la probabilité de présence de l’électron en un point donné.
L’élément de probabilité dans un élément de volume est de la forme :
dP
= y2dV
La densité de probabilité s’écrit donc :
![]()
On ne parle plus de localisation de l’électron mais de probabilité de présence. L’électron est donc caractérisé par la fonction d’onde .Celle-ci a trois critères :
- L’électron se trouve forcément quelque part, pour un
rayon infini, la probabilité est 1 :![]()
(condition de normalisation)
-
La fonction d’onde est régulière (continue).
- La fonction d’onde doit être uniforme,
en 1 point de l’espace, il n’y a q’une seule valeur de
probabilité (la fonction d’onde décrit un seul électron)
Dans l’atome d’hydrogène, il y a une symétrie sphérique, il est donc plus simple de se servir des coordonnées sphériques : M(x,y,z) Þ M(r,q,j)
q varie de 0 à p (angle vertical), j de 0 à 2p (angle horizontal), r le rayon.
ainsi :
x = r sinq cosj
y = r sinq sinj
z = r cosq
D’après Pythagore, on peut aussi dire r²=x²+y²+z²
2) Orbitales monoélectriques H et hydrogénoïde :
La fonction d’onde Y est aussi appelée orbitale.
On peut décomposer la fonction d’onde comme suit :
Y (r,q,j) = R(r) * Q (q) * F (j)
Cette équation fait intervenir ce qu’on appelle les nombres quantiques :
R dépend de n et l
Q dépend de l et ml
F dépend de ml
n, l et ml sont des entiers dans Z.
2 - 2' :Nombres quantiques :
n, le nombre quantique principal :
n , expression de l’énergie de l’électron (si n=1, pas d’excitation)
Ce nombre définit le volume dans lequel l’électron peut se situer. n défini également la couche électronique.
l, le nombre quantique secondaire ou «orbitale» :
sa valeur est liée au nombre n : 0<l<n-1. Ce nombre permet de définir la forme du volume dans lequel se trouve l’électron.
ml, le nombre quantique magnétique, s’écrit ml parce qu’il dépend de l : -l ≤ ml ≤ l
La combinaison de ces 3 nombres quantiques définit l’état de l’électron. A l’état fondamental on a n=1, donc l=0, donc ml=0.
On écrit la fonction d’onde associée à cette état «Y100».
Si n>1, il existe alors plusieurs combinaisons de nombres quantiques. A chaque combinaison, on associe une fonction d’onde différente.
Dans un atome, il y a plusieurs couches électroniques : Cette couche est définie par le nombre n, donc chaque couche a une énergie différente.
Le nombre l défini la sous couche de l’électron. Les énergies des sous couches sont sensiblement différentes.
|
n |
couche |
sous
couche |
|
1 |
K
|
s |
|
2 |
L |
s et p |
|
3 |
M |
s, p et d |
|
4 |
N |
s, p , d et f |
Les différentes orbitales :
pour chaque sous couche déterminée (avec n et l), il y a ml orbitales différentes... (c’est à dire ml orientations possibles de la trajectoire de l’électron)
Ex :
Y211: n=2,
l=1, ml=1 : rotation dans la couche L, sous couche s, et autour de l’axe
y.
Y210: rotation
autour de l’axe z
Y211: rotation
autour de l’axe x (![]() )
)
Représentation des orbitales électroniques :
Pour définir une orbitale, on représente sa variation de densité électronique en fonction de sa distance au noyau. On exprime Y² en fonction de r.
Pour cela on a besoin de l’élément de volume en coordonnée polaire :
dV= r² sinq dq dj dr
Type :pour intégrer cela, on sépare la triple intégrale en produit de trois intégrales simples :
11H+31T è 42He + E
Mathématiquement,
Le volume d’une sphère de rayon r (r variant de 0 à r final, q varie de 0àp, et j de 0à2p)
Ex : étude de l’orbitale 2s : (Y200)
l’énergie de l’électron est celle de n=2 : donc -13.6/2² = -3.4 eV
On nous
donne la fonction d’onde associée à 200 : ![]()
cette fonction d’onde ne dépend que de r, elle prend la même valeur pour tout point d’une même sphère.
On cherche à connaître la densité de probabilité d’un électron en fonction de r :
Comme en maths pour étudier une fonction, on étudie la fonction dp=Y22s dV. On étudie la fonction en calculant la dérivée /dV qui s’annule en 2 et en 4, et on constate que :
- lim de dp en 0 est
maximale : la densité de probabilité est maximale plus près du noyau.
- dp(2)= 0, il n’y
a donc jamais d’électrons à 2 ula (surface
nodale (sous entendu la surface de la sphère de rayon r=2)).
- en +infini, dp=0,
plus on s’éloigne, moins il y a de probabilité de trouver un électron.
Le gradian de densité est irrégulier en fonction de la distance au noyau !
Le nuage électronique est inhomogène.
Une liaison se fait entre 2 atomes quand 2 électrons se touchent. Si on considère 2 atomes comme on vient d’étudier, il ne pourront pas se lier si la distance entre les noyaux est égale à 4 (car dans ces cas la, les points de contact seront les 2 sphères de rayon 2, et il n’y a pas d’électrons dans ces sphères pour cette orbitale !
Calculons la densité radiale de probabilité:
![]() . On étudie cette fonction:
. On étudie cette fonction:
on trouve 0 pour r=2 et maximum pour r un peu plus petit que 6.
Calculons le rayon de la sphère tel que la probabilité de présence soit de 90%. R=9.1 ula
Le rayon croît avec le nombre quantique principal.
Pour tracer les orbitales :
pour représenter d’autres orbitales, avec des q et des j, on pause une valeur pour j, et une valeur pour r, ensuite , on trace le graphe de z en fonction de x par exemple, en faisant des conversions, et en faisant varier q, on obtient ainsi la trajectoire de l’orbitale.
Equation de Schrödinger généralisée :
dans le cas d’un atome qui contient 2 ou + électrons, c’est trop dur
Energie :
Les orbitales ont des énergies : il y a une règle pour déterminer l’énergie : (on dit qu’il y a dégénérescence des niveaux quand il y a des orbitales atomiques qui ont la même énergie)
Pour l’hydrogène
et les hydrogénoïdes :l’énergie ne dépend que du nombre quantique
principal : ![]() . Dans ce cas, la dégénérescence pour chaque valeur de
n est égale aux nombres de combinaisons pour l et ml, donc du nombre d’orbitales
pour chaque valeur de n (1 pour
n=1, 4 pour n=2, 9 pour n=3 ...)
. Dans ce cas, la dégénérescence pour chaque valeur de
n est égale aux nombres de combinaisons pour l et ml, donc du nombre d’orbitales
pour chaque valeur de n (1 pour
n=1, 4 pour n=2, 9 pour n=3 ...)
Pour tous les autres
atomes : les sous couches ont des énergies différentes, la dégénérescence
dépend donc de l (1 pour n=1, 2 pour n=2, 3 pour n=3, 4 pour n=4 ...)
|
n |
nom de
la couche |
l |
nom de
la sous couche |
nombre
d’orbitale par sous couche |
Nombre
d’orbitale par couche |
dégénérescence |
|
1 |
K |
0 |
s |
1 |
1 |
1 |
|
2 |
L |
0 1 |
s p |
1 3 |
4 |
2 |
|
3 |
M |
0 1 2 |
s p d |
1 3 5 |
9 |
3 |
|
4 |
N |
0 1 2 3 |
s p d f |
1 3 5 7 |
16 |
4 |
représentation des couches d’énergie , par ordre croissant d’énergie:
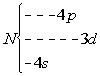
![]()
![]()
![]()
Plus on monte, plus l’atome a de l’énergie interne...
La règle de Klechkowski :
on classe les différentes couches (avec sous couche) par ordre croissant de la somme de leur nombre n et l (ainsi la couche 3d (3 + 3=6 ) est plus éloignée de la couche 4s (4 + 1=5))
l’énergie d’une sous couche croît donc avec la somme de n et l.
Structure électronique des atomes :
On appelle structure électronique ou configuration la répartition des électrons d’un atome dans les différentes orbitales.
On défini pour cela le 4è nombre quantique, le nombre quantique de SPIN. (symbolisé ms)
Les 3 premiers nombres quantiques permettent de calculer la fonction d’onde en tout point de l’espace (caractérisent l’électron dans un volume)
Le 4è caractérise l’électron tout seul : l’électron tourne sur lui même dans un sens ou dans l’autre : ms défini le sens, il prend donc la valeur «1/2» ou «-1/2».
Les 3 règles de configurations électronique :
règles de stabilité maximum : un électron est d’autant plus stable que son énergie est basse : on commence par remplir les couches d’électron par le début : 1s, 2s, 2p, 3s, 3p, 4d, 3d .... (on respecte bien la règle de Klechkowski)
Règle d’exclusion de Pauli : chaque atome est caractérisé par 4 nombres quantiques, aucun électron n’a la même combinaison avec son voisin. (on comprendra alors facilement qu’il n’existe que 2 électrons maxi sur 1 orbitale)
Règle de Hund : quand on a des orbitales de même énergie, et qu’on a pas assez d’électrons pour toutes les combler, on commence par en mettre un dans chaque orbitale en question, on complète ensuite.
Représentation par un schéma :
Dans la représentation des couches d’énergie, on place des flèches vers le haut et vers le bas sur les traits horizontaux des orbitales. (un sens défini le nombre ms, choisi arbitrairement)
C’est la représentation la plus riche qui permet de voir toutes les propriétés de l’atome.
Représentation linéaire :
ex : cas de l’azote (Z=7) :
![]() c’est à dire : 2 électrons (en puissance) dans la 1s,
2 dans la 2s, 3 dans la 2p
c’est à dire : 2 électrons (en puissance) dans la 1s,
2 dans la 2s, 3 dans la 2p
on peut également remplacer une partie de l’expressions linéaire d’un élément en utilisant l’expression linéaire d’un gaz pur (dernière colonne du tableau périodique) :
Par exemple, la Calcium pourra s’écrire :
« 1s² 2s² 2p6 3s² 3p6 4s2 » ou encore « [Ar] 3s² 3p6 4s² » (l’argent (Ar) est un gaz rare)
mais on peut aussi l’écrire :
Y100, cela veut dire que les couches K et L (1 et 2) sont complètes
Représentation de Lewis :
on fait figurer autour de l’atome les électrons de valence (ceux de la dernière couche (ou encore de la même ligne du tableau périodique que celle qui comporte l’élément étudié))
Calcium :
![]() : 2 électrons de valence Azote :
: 2 électrons de valence Azote : ![]() : 5 électrons de valence.
: 5 électrons de valence.
Modèles des cases quantiques :
pour chaque sous couche, on dessine des «carrés collés», avec des flèches à l’intérieur : une vers le haut , une autre vers le bas (quand il y a des électrons). Pour un même niveau d’énergie, ont remplira toujours en premier toutes les flèches qui vont vers le haut… puis celles qui vont vers le bas (en fonction du nombre d’électrons existants)
on sépare les carrés, des autres sous couches, par un espace.
Modèle de Slater :
la dégénérescence est plus faible dans un atome quelconque que dans un atome d’hydrogène : dans un atome quelconque, un électron est soumis a la force du noyau mais aussi par celle de ses collègues.
Dans un atome quelconque donc, les électrons font un écran entre l’électron considéré et le noyau, l’électron a alors une charge efficace Zx = Z - s (s = constante d’écran)
l’énergie
de l’électron sera alors calculée ![]()
la constante s dépend de la sous couche ou de l’orbitale sur laquelle se trouve l’électron mais aussi de la présence des autres électrons.
Dans un atome, chaque électron a sa constante d’électron.
type : avec Slater, on détermine l’énergie d’un électron
spécifique dans un atome.
les électrons des 2 premières couches ont la même énergie, on
les regroupe donc. On écrira alors un atome sous la forme (1s)²
(2s2p)8 (3s3p)8 (3d)(4s)²
exercice type :
l’atome de carbone , z = 6 , on veut l’énergie d’un
électron 1s, et celle d’un électron 2s2p.
On donne, pour un électron de :
•
la
couche 1s, les collègues ont un s de 0.31, les autres 0
•
la
couche 2s2p, les collègues ont un s de 0.35, ceux de la couche 1s ont un s de 0.85
(valeurs empiriques)
résolution :
on écrit l’atome avec le format de Slater : 1s²2s²2p²
è (1s)² (2s2p)4
Calculons l’énergie d’un électron de 1s :
il a 1 collègue, et ceux de la couche 2s2p n’interviennent
pas, donc s = 1 * 0.31
donc avec la relation de la page précédente, on trouve l’énergie
de l’électron :
Ee(1s) = - 446 eV (c’est
a dire l’énergie d’un électron 1s)
l’énergie d’un électron 2s2p : il a 3 collègues
et il y a 2 électrons dans 1s, donc
s = 3 * 0.35 + 2 * 0.85, donc Ee(2s2p)
= -35.9 eV
L’énergie d’ionisation :
c’est l’énergie nécessaire pour arracher un électron de son atome.
exercice type :
on écrit la réaction : C è C+ + e- +I (I est l’énergie d’ionisation)
on peut donc écrire : I = EC+ -
EC (I est positif
è attention au sens de C+
et C)
On calcule donc grâce à l’exercice type précédent les énergies d’un électron de C et de C+, et on additionne tous les électrons pour avoir l’énergie de l’atome... Mais comme on soustrait les 2 ensuite, il est inutile de calculer les couches identiques (on ne calcul donc que la dernière) Pour le C, on ne calcule que Ee(2s2p) et pour C+ Ee(2s2p) (qui ne sont pas les mêmes car C+ a moins de collègues !!)
On peut donc se ramener à I = 3Ee2s2p –
4Ee2s2p donc I = +
11.6 eV
Source : www.fvirtman.fr.st
– Auteur : Fman
ÓSNOCLUB.fr.st