| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© snoclub.fr.st
I Raisonnnement mathématique
I.1 Utiliser la tautologie
(a->b) <-> (non b -> non a)
c'est montrer la contraposée.
exemple :
f injective :
c'est montrer que si x1
<> x2 => f(x1) <> f(x2)
c'est équivalent à f(x1) = f(x2) => x1 = x1
I.2 Raisonnement par l'absurde
C'est utiliser la tautologie
P <-> (non P -> Ø )
I.3 Analyse de cas
G <-> ( (F->G) ^ (non F -> G) )
II Fonctions booléennes
II.1 Définition
Une fonction booléenne à n variables est une application de {0,1}n dans {0,1}
f : {0,1}n -> {0,1}
(x1, x2, ..., xn) -> f(x1, ..., xn)
xi = variables booléenns (appartiennent à {0,1} )
A chaque proposition
P(P1, ..., Pn) (Pi = variables propositionnelles)
correspond une fonction booléenne définie par
fp (x1, ..., xn) = ![]() (P(P1, ..., Pn))
(P(P1, ..., Pn))
avec xi = ![]() P(i) pour i = 1, ..., n
P(i) pour i = 1, ..., n
exemple :
P le ^
f^ (x,y) = ![]() (X ^ Y) avec x =
(X ^ Y) avec x = ![]() (X)
et y =
(X)
et y = ![]() (Y)
(Y)
II.2 Forme polynomiale d'une fonction booléenne
On pose par convention
f^(x,y) = x * y
et
fv(x,y) = x + y (ne corresponde pas à l'addition dans Z : 1 + 1 = 1)
fnon(x) = 1 - x = ![]()
En utilisant ces conventions, toute fonction booléenne de 2 (resp n) peut s'écrire sous forme d'un polyome de degrés au plus 2 (resp n)
Quelques propriétés :
x * x = x
x + x = x
x + ![]() = 1
= 1
(x + y)b = xb yb
b signifis barre
(xy)b = xb + yb
xy + xyb = x (y + yb) = x
II.3 Forme Normale Disjonctive
Définition : On appelle fonction produit (ou monome canonique ou minterme) un produit de n facteurs obtenus en choisissant pour tout i un seul facteur xi ou xib
Cas général
= PI(i=1 à n) (ai xi + (1-ai) xib ) ai appartient à {0,1}
exemple : n=2 2 variables booléennes x et y
les mintermes sont : x y, x yb, xb y, xb yb
Il y a 2n mintermes
Propriété : toute fonction booléenne peut s'écrire de manière unique sous la forme d'une somme de monomes canoniques. C'est la forme normale disjonctive
exemple :
f(x,y) = xb y + x y
II.4 Notion de circuits logiques
a) Portes
0 : pas
de tension
1 : 1 tension + xV
A chaque fonction booléenne de base correspond une porte logique
exemple :
et : "AND"
![]()
ou : "OR"
![]()
xb
![]()
Non - ou : NOR
![]()
Non et : NAND
![]()
b) Méthode de Karnaugh
C'est une méthode pour simplifier une fonction booléenne basé sur x y + x yb = x
Tableau de Karnaugh : C'est la représentatio d'une table de vérité sus la forme d'un tableau tel que : une seule variablle boolenne change d'état lorsque l'on passe d'une ligne (ou d'une colonne) à la suivante
n=2
f(x,y) = xb y + xy
n= 4
f (x, y, z, t ) = xb yb zb tb + xb yb z t + xb yb z tb + xb y zb tb + x y z t + xb y z tb + x yb zb tb + z yb zb t
c) Méthode
On cherche dans le tableau de Karnaugh les groupements de 2, 4, 8, ..., 2n consécutifs; dans chaque groupement on supprime les variables booléennes qui changent d'état
Attention :
la première ligne (colonne) est consécutive à la dernière ligne
(colonne)
Un même élément peut servir plusieurs fois
f(x,y,z,t) = xb z + xb tb + x yb zb
1
2 3
exemple 2 :
g(x,y,z,t) = t
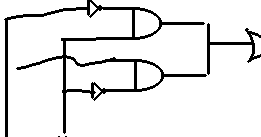
exemple de fonction logique :
f(x,y) = xb y + x yb = x ![]() y
y
Source : www.fvirtman.fr.st
– Auteur : Fman
ÓSNOCLUB.fr.st