| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
Exercice type : (culture : c’est la suite de Fibonacci)
![]()
![]()
Exprimer a en fonction de
n pour calculer plus facilement un terme de la suite
On se sert de ce qu’on appelle une fonction génératrice.
On pose : 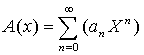 :
formule à apprendre.
:
formule à apprendre.
On a : ![]() ,
on va essayer de faire apparaître A(X). Idée, on multiplie tout par
,
on va essayer de faire apparaître A(X). Idée, on multiplie tout par ![]()
![]()
(on essaie de faire apparaître les mêmes coefficients
pour les a et les X associés, en multipliant par X et X²)
Il ne manque plus que le Sigma (![]() )
qui va à l’infini.
)
qui va à l’infini.
Idée : écrire les équations
avec différentes valeurs pour n (car c’est le n qui change dans le
sigma), puis de tout ajouter. On a :
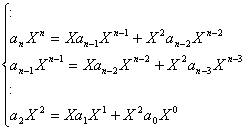 ,
(les n continuent jusqu’à l’infini)
,
(les n continuent jusqu’à l’infini)
(on
comprend bien qu’on ne peut pas descendre plus bas, sinon, on aurait
des a(-1) =>interdit)
Si
on additionne toutes ces lignes puis qu’on arrange, on obtient :
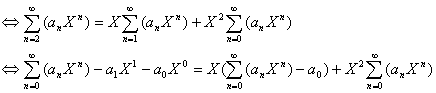
Quand
on a un Sigma qui part par exemple de 1 et qui va à l’infini, on
peut remplacer le tout par un sigma qui part de 0, et enlever par la suite
le terme n=0, ça revient au même. (cela explique le passage de la 1e
ligne à la 2e ligne ci dessus).
Maintenant,
on a fait apparaître les A(X) !
![]() .
.
Je
vous fait confiance pour remplacer les a1 et a0 par leurs valeurs données
et isoler les A(X) on a :
![]()
Il
faut simplifier ceci en réduisant cette fraction en petites fractions
simples :
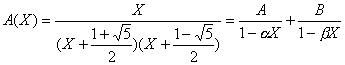 (on
factorise le dénominateur avec
(on
factorise le dénominateur avec ![]() )
)
(attention,
les dénominateurs des petites fractions doivent être 1- aX, sinon, bidouiller)
Il
faut donc mettre A(X) sous cette forme. Ensuite, il faut trouver A, B,
![]() et
et ![]() ,
on applique la technique vu dans le chapitre « polynômes »
,
on applique la technique vu dans le chapitre « polynômes »
On a la solution
générale :
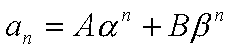 (apprendre
cette formule)
(apprendre
cette formule)
Dans cet exercice, la solution générale est 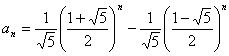
ÓSNOCLUB.fr.st