| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
Exercice type 1
:
Soit la fonction paramétrique suivante : 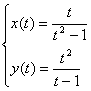
1) Voir le Domaine de définition.
2) Etudier les symétries.
3) Tracer le tableau de variation,
4) puis la courbe.
1) Type : Trouver les valeurs pour lesquelles x(t) ou y(t) n’existe pas
Pour x(t), t ne doit pas prendre les valeurs –1
et 1. Pour y(t), éviter 1. En somme, la courbe paramétrique existe seulement
pour ![]()
2) Type : rechercher la parité ou l’imparité de x(t)
et y(t) -> calculer x(t) et y(t)
Théorème 1
:
Si pour une courbe f(x), f(x) = f(-x) alors
la courbe est paire.
Si pour une courbe f(x), f(-x) = - f(x), alors
la courbe est impaire.
Ici ![]() et
et ![]() ,
donc x(t) n’est ni paire ni impaire. De même pour y(t).
,
donc x(t) n’est ni paire ni impaire. De même pour y(t).
Il n’y a aucune symétrie d’axe Ox, ni d’axe
Oy, ni de centre O. (Voir tableau en dessous)
FAQ :
Et si il y a des fonctions paires ou impaires ? -> Si l’une
des fonctions x ou y n’est ni paire ni impaire, on est dans le même
cas, sinon, voir tableau.
FAQ :
Aucune symétrie par Ox, Oy ou O, c’est tout par rapport à O. Et si
on veut trouver une autre symétrie ? -> On décentre ! On change de repère :
Ex : x(t) = t + 2 n’est ni paire ni impaire. Posons X(t) = x(t) –2, alors X(t) est impaire ! Il est pratique dans ce cas de changer de repère. (et alors les symétries éventuelles se feront par rapport à un point d’abscisse –2)
Note : décentrer que si le changement de repère crève les yeux, sinon, c’est pas grave !
|
Symétries |
y(t) paire |
Y(t) impaire |
|
x(t) paire |
? |
Symétrie par rapport à Ox |
|
x(t) impaire |
Symétrie par rapport à Oy |
? |
3)
Type : comme en terminale,
on cherche x’(t) et y’(t), on étudie le signe, et on cherche
les limites au bout de chaque branche (flèche).
On calcule : ![]()
![]()
t
-i -1 0 1
2 +i
![]()
x’ - - - -
![]()
![]()
y -i
--1/2 0
-i +i
4 +i
![]()
y’ + + 0 - - 0
+
Tracer un tableau de variation n’est pas ce qu’il y a de
plus dur, on calcule les limite ou les valeurs aux points intéressants
(ceux ou on change de flèche), mais aussi ceux ou
l’autre fonction change de direction (comme le 2/3 de la fonction
x à t=2 par exemple, car y change de direction à ce moment la.)
Recherche d’asymptotes :
Il n’est pas facile de tracer une courbe paramétrique, alors
déjà on a pas mal d’informations avec le tableau, mais il est important
de connaître des asymptotes !
Comment on fait pour trouver toutes les asymptotes ?
On regarde les branches infinies (c’est à dire les branches
(les flèches) qui on une extrémité vers + ou – l’infini). On
récupère les valeurs de t correspondantes à ces extrémités infinies.
·
t à -infini x(t) à 0 et y(t) à -infini à on a une asymptote
x=0 verticale
(quand x(t)àconstante et y(t)à+/-infini, alors
on a une asymptote x=constante.)
·
tà-1 x(t)à infini et y(t)
à-1/2 à dans ce cas, asymptote
y=-1/2
·
tà+infini asymptote x=0
·
tà1 x(t)àinfini et y(t)àinfini, dans ce
cas, on a surement une asymptote oblique : voilà comment on la trouve
:
on calcule ![]() .
A t = 1 (la valeur de t que l’on étudie), t(t-1)à2
.
A t = 1 (la valeur de t que l’on étudie), t(t-1)à2
Donc a t = 1, y(t)/x(t)à2, Type : On ramène
tout d’un seul coté et on recalcule la limite.
FAQ : si ça
tend vers +/-infini ? => oublie l’asymptote.
y(t)/x(t)à2 ó y(t) à 2x(t) ó y(t) – 2x(t) à ?
(Ca y’est, on a tout ramené du même coté comme si le à était un = . Mais
la, il ne faut pas dire qu’à droite on met 0 comme avec un = )
On recalcule la limite, on a y(t) – 2x(t) à 3/2
On ramène à nouveau tout du même coté ! y(t) – 2x(t) –3/2 à ?
Et la on trouve 0 !
FAQ : et si
on ne trouve pas 0 ici ? => déjà, je ne sait pas si c’est
possible, puis sinon, oublie l’asymptote. De toute façon, ces calculs
servent uniquement à tracer une courbe plus juste.
Donc pour t = 1, y(t) – (2x(t) +3/2) à 0
Et bien ce 2x(t) +3/2, c’est l’équation de l’asymptote
qu’on cherchait. y = 2x + 3/2
Note : A t = 1-, la limite de y(t) – (2x +3/2) est négative
à la courbe est
sous l’asymptote.
A t= 1+, la limite est positive, la courbe sur (au dessus de) l’asymptote.
4) la courbe , type : on trace bien les asymptotes
aussi :
spécifiques. 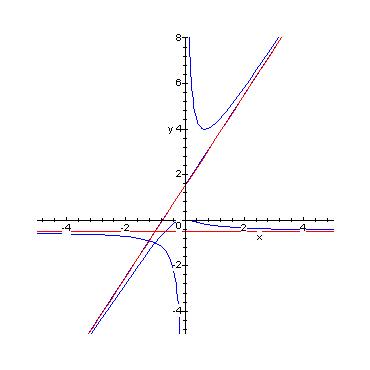
Types : comment
trouver des points d’intersections (on en voit plein sur le graph) ?
Première chose à faire : trouver la valeur t du point d’intersection cherché.
·
Un point de la courbe coupant une asymptotes horizontales ou verticales à on connaît alors
c tel que x(t) = c ou y(t) =c. On résout donc ! Attention à trouver
des t dans le domaine de définition !
·
Un point coupant des asymptote oblique à on sait alors
que y(t) – (ax(t)+b) = 0. Ou a et b définissent l’asymptote
oblique, et on connaît a et b. On résout donc.
·
Un point de la courbe coupant un autre point de la courbe (appelé
point double)à on sait alors que l’on doit trouver t et s différents
tels que x(t) = x(s) et y(t) = y(s) . C’est un système. (des fois
ultra chiant à résoudre)
Deuxième étape : une fois qu’on a t, les coordonnées du point sont (x(t), y(t))
Ici, on a M(-2/3,-1/2) qui est un point de la courbe coupant l’asymptote
Y=-1/2, N(-6/5,-9/10) coupant l’asymptote oblique y=2x+3/2, et A(-1,1)
ou 2 valeurs de t différentes passent par la.
Exercice type 2 :
Cet exercice est moins détaillé mais va droit au but (comme Sony
Anderson)
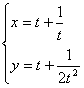
Domaine de définition :
x(t) n’existe pas pour t = 0, y(t) n’existe pas pour t
= 0 à domaine de def
= R \ {0}
Symétries :
x(t) est impaire, mais y(t) n’est ni paire ni impaire à vite torché :
pas de symétrie évidente
Tableau de variation :
Je vous laisse le dessiner.
![]() ,
et
,
et ![]()
Points singuliers :
et ou sont les points pluriels ? (ahah !qu’il
est drôle !)
Un point singulier est un point ou x(t) et y(t) s’inversent. C’est un pic sur la courbe. Recherchons les points singuliers :
Formule : on cherche les t vérifiant x’(t) = y’(t) = 0 pour connaître les points singuliers
t = 1 vérifie cette formule, donc S (x(t = 1), y(t = 1)) est un point
singulier S (2,3/2)
C’est la seule solution, t = 1, on a donc qu’un seul
point singulier. (on peut en avoir 0 ou 150)
Fonction « pente de la tangente »
On peut avoir la pente de la tangente à la courbe étudiée pour n’importe
quelle valeur de t !
Formule :
la fonction « pente de la tangente » se calcule ![]()
La pente de la tangente au point singulier est m(t = 1) = 3/2
Recherche des asymptotes :
On regarde les branches infinies dans le tableau de variation que
je n’ai pas fait. (si, je l’ai sous les yeux en fait, dégueulasse
au brouillon, mais je l’ai)
·
t= - infini à x(t)= infini,
y(t) = infini
Formule :
pour trouver une asymptote oblique, on calcule ![]() au
point donné, expliqué mieux dans exercice type 1.
au
point donné, expliqué mieux dans exercice type 1.
Ici, la limite en – infini tend vers 1, on ramène tout a gauche,
on calcule la limite de
y(t)-1*x(t) à 0. Pas la peine
d’aller plus loin, on a notre asymptote oblique y = x.
·
t à 0 . x(t) à infini, y(t) à infini. y(t)/x(t)à infini. STOP ! pas d’asymptote ici. (il faut que ça tende
vers une constante !)
·
tà + infini . x(t)àinfini, y(t)àinfini. On constate
vite ici qu’on fait le même calcul qu’en –infini, donc asymptote
y=x
Recherche des points
doubles :
On
cherche à résoudre le système ![]() avec t différent de s pour trouver les points doubles.
avec t différent de s pour trouver les points doubles.
Ici, on ne trouve pas de solutions ! On constate donc qu’il
n’y a pas de points doubles !
(mais alors quel bordel à résoudre, ce système)
Points d’inflexion ou de concavité
C’est quand la pente de la tangente change de direction.
Graphiquement, à l’inflexion, on se met à tourner à droite (RESP
concavité : à gauche)
TABLEAU A FAIRE
la pente de la tangente était croissante , puis à partir de –1/2,
elle change de direction.
On dit que ce point tel que t = -1/2 est un point d’inflexion de la courbe (la tangente a alors comme
pente –3), car il c’est un maximum (RESP concavité quand minimum)
Points de rebroussements :
On a un point singulier, c’est donc un point de rebroussement
Pour t = 1, m(t) = 3/2. A t = 1, on voit bien que la pente de la
tangente est déjà en train de décroître et continue. Elle n’est ni
minimum, ni maximum. Si cette pente avait été minimum pour le point S, alors on aurait
eu un truc du genre :
Courbe : (On récupère toutes les informations)
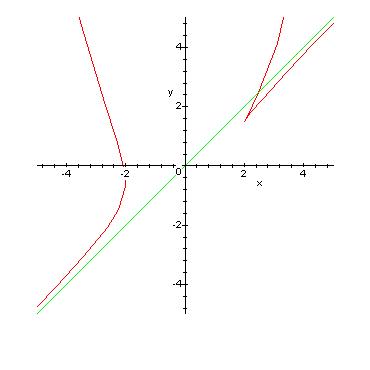
Source : www.fvirtman.fr.st
– Auteur : Fman
ÓSNOCLUB.fr.st