| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
I – Les équations
différentielles de degré 1 :
Structure :
![]() (1)
(1)
a(x)
et h(x) sont des fonctions de x données,
f(x) est la fonction inconnue.
Si l’équation n’est pas de cette forme, s’y ramener.
Algorithme de résolution :
Les
solutions s’écrivent ![]() (S)
(S)
Trouvons g(x) :
g(x)
est une solution de l ‘équation de référence ![]() (2)
(2)
on
retiendra que :
![]() ,
,
![]() est un réel quelconque, A(x) est une primitive de a(x)
est un réel quelconque, A(x) est une primitive de a(x)
Trouvons f1(x) :
![]() est
une solutions particulière de (1)
est
une solutions particulière de (1)
![]() (3)
(3)
On
calcule ![]() ,
puis on remplace dans (1) : tous les
,
puis on remplace dans (1) : tous les ![]() s’en
vont, sinon c’est faux ! !
s’en
vont, sinon c’est faux ! !
De
la, on trouve la valeur de ![]() .
On le primitive pour trouver
.
On le primitive pour trouver ![]() ,
on remplace dans (3) pour retrouver
,
on remplace dans (3) pour retrouver ![]() ,
qu’on remplace dans (S) pour trouver f(x)
,
qu’on remplace dans (S) pour trouver f(x)
Note : ![]() est une solution quelconque de (1), ne se cassons pas la tête avec
les constantes pour les primitives, on peut les ignorer (donc dire qu’elles
valent 0)
est une solution quelconque de (1), ne se cassons pas la tête avec
les constantes pour les primitives, on peut les ignorer (donc dire qu’elles
valent 0)
II– Les équations
différentielles de degré 2 :
Structure :
![]() (1)
(1)
a et b dont des réels donnés , h(x) une fonction de x donnée, f(x)
est la fonction inconnue.
Algorithme de
résolution :
Les solutions s’écrivent ![]() (S)
(S)
Cherchons g(x) :
g(x) est solution de l’équation de référence ![]() (2)
(2)
Ramenons cette équation au polynôme du 2è degré ![]() (E)
(E)
On calcule ![]() ,
ainsi que la ou les racines
,
ainsi que la ou les racines ![]() dans
R ou dans C (
dans
R ou dans C (![]() et
et ![]() réels quelconques)
réels quelconques)
·
![]() :
: ![]()
·
![]() :
:
![]()
·
![]() : on a des racines sous la forme
: on a des racines sous la forme ![]() ,
et on a, dans ce cas :
,
et on a, dans ce cas :
![]()
Cherchons f1(x) :
![]() est une solution particulière de (1)
est une solution particulière de (1)
Tout dépend de la structure de h(x)
Cas A : h(x) est un polynôme :
Soit n le degré de h(x)
![]() sera aussi un polynôme
sera aussi un polynôme
·
de degré n si b<>0
·
de degré n+1 si b=0 et a<>0
·
de degré n+2 si a=b=0
On écrit ![]() sous
forme du polynôme avec des inconnus comme coefficients. On calcule aisément
sous
forme du polynôme avec des inconnus comme coefficients. On calcule aisément
![]() et
et ![]() qu’on inclue dans (1), on procède par identification pour trouver
qu’on inclue dans (1), on procède par identification pour trouver
![]() .
Si un coefficient peut prendre une valeur quelconque, on lui en donne
une simple (c’est une solution quelconque), ne l’oublions pas !
.
Si un coefficient peut prendre une valeur quelconque, on lui en donne
une simple (c’est une solution quelconque), ne l’oublions pas !
Cas B : h(x)
est de la forme ![]() (n réel donné, P(x) fonction polynôme)
(n réel donné, P(x) fonction polynôme)
On pose ![]() tel que
tel que ![]() (B)
(B)
On calcule les dérivées premières et seconde de ![]() et on remplace dans (1), on factorise par
et on remplace dans (1), on factorise par ![]() ,
afin de virer ces derniers dans les 2 membres. On est ramené au cas A
avec
,
afin de virer ces derniers dans les 2 membres. On est ramené au cas A
avec ![]() au
lieu de
au
lieu de ![]() ,
on n’oubliera pas de bien récupérer ce dernier avec (B)
,
on n’oubliera pas de bien récupérer ce dernier avec (B)
Cas C : h(x)
est de la forme P(x)cos(nx)+Q(x)sin(nx) (avec
P(x) et Q(x) polynômes, n réel)
Est ce que ![]() *n
est racine complexe de (E) ?
*n
est racine complexe de (E) ?
·
non :
![]()
·
oui :
![]()
Dans ces 2 cas, U(x) et V(x) sont des polynômes de
même degré que P(x) et Q(x), on calcule la dérivée première et seconde
de ![]() ,
on résout (1) par identification.
,
on résout (1) par identification.
Cas D : h(x) est de la forme de C multiplié par ![]()
On procède comme en B en posant un z. On se réfère
ensuite au cas C.
Autres cas :
On essaie de transformer h(x) en une somme finie de cas qu’on connaît.
Et donc 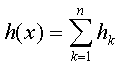 (n
est le nombre de petites fonctions sommées dans h(x))
(n
est le nombre de petites fonctions sommées dans h(x))
On
résout alors pour chaque k , ![]()
Et 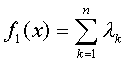
Et au fait , il faut conclure ! !
Une fois ![]() trouvé, on oublie pas de remplacer dans (S)
trouvé, on oublie pas de remplacer dans (S)
Et si rien ne marche ?
T’essaie d’assurer dans les autres exercices pour amortir les dégâts…
Mais marque toujours « pas de solutions », il se peut que ce soit ça, mais n’y compte pas trop..
ÓSNOCLUB.fr.st