| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© SNOCLUB.fr.st
hypothèse du chapitre : régimes alternatifs sinusoïdaux de basse fréquence
On
considère que l'intensité est la même en tout point d'une branche considérée
I - Expressions instantanées des intensités et des courants
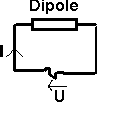 |
u(t)= Um cos wt u(t) appartient à [-Um, +Um] Um = amplitude de la tension -Um, + Um sont les valeurs crête à crête w = pulsation rad.s-1 |
On
fixe un sens arbitraire de U mais I est imposé par la convention générateur
i = im cos (wt -j)
w
est le même que U d'où un régime forcé
Mais
i n'a pas la même phase (j) => Déphasage
w
= 2p/T
avec
T = période : temps au bout duquel le temps se reproduit de façon identique
à lui-même (en s)
et
f = 1/T : fréquence : nombre de fois dont le phénomène se reproduit de
façon identique à lui-même en une seconde (Hertz)
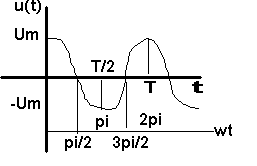 |
U=Um cos wt <=>
u origine des phases - Si j>0, i est en retard sur U - Si j<0, i est en avance sur U |
=>
Si on fait un changement d'origine des temps avec wt' = wt-j
alors
U
= Um cos(wt'+j)
i = Im cos wt'
Déphasages
remarquable :
Si
j=0 U
et i sont en phase
Si
j=p U
et i sont en opposition de phase
Si
j=± p/2 U et I sont en quadrature
j= w(t - t') = 2p
(t-t') / T
II - Valeurs efficaces des courants et tensions
![]()
u = Um cos wt
i = im cos (wt-j)
Puissance
instantanée dégagée par effet joule
p(t)= Ri² = R im² cos²(wt-j)
<p(t)>
est une période T = 1/T 0òT p(t)dt
= 1/T 0òT R im² cos²(wt-j) dt
= Rim²/T 0òT cos²(wt-j)dt
cos 2o = cos²o - sin²o
=> cos ²o = (1 + cos 2o)
/ 2
= Rim²/2 + Rim²/T [ sin 2(wt-j) - sin (-2j) /w]
= 0
<p(t)>
= Rim²/2
En
continu, l'intensité I nécessaire pour produire la même puissance vérifie
:
<P>=Ri²
On
appelle intensité efficace I (ou Ieff), l'intensité d'un courant continu
qui produirait la même puissance qu'en alternatif.
I² = Im²/2 => I = Im / Ö2
On
généralise aux tensions => Ueff
: U = Um / Ö2
u(t) = Um/u Ö2 cos wt
i(t) = I Ö2 / im cos (wt -j)
Les
appareils en alternatifs mesure
en continu (=, DC)
en alternatif (~,AC) -> valeurs efficaces
1)
Résistance
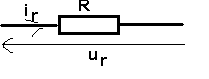
Ur(t)
= R ir(t)
Ur
= Ur Ö2 cos wt
= im cos(wt-j)
} jr=0
= ir Ö2 cos(wt-j) }
Aux
bornes d'une résistance u et i sont en phase
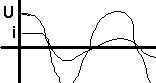
2)
Bobine parfaite
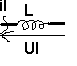
Ul
= L di/dt <=> il=ò (Ul Ö2 / L) cos wt dt = ul
Ö2 / L (sin wt) / w
Ul = Ueff sqr(2) cos wt} <=> ( Ul 2) / Lw ) cos(wt - p/2)
il=
Il sqr(2) cos wt}
Il
= Ul / lw
j= + p/2
Aux
bornes d'une bobine, i et en quadrature retard sur u
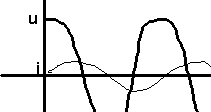
3)
Condensateur parfait
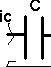
uc
= Uc sqr(2) cos wt
ic = Ic sqr(2) cos (wt-j)
q=Cuc } ic
= C duc/dt => ic = C Uc sqr(2)
(-wsin wt)
i = dq/dt}= c w Uc sqr(2) cos(wt+ p/2)
Aux
bornes d'un condensateur, i est en quadrature avancée sur U
Ic
= C w Uc }
Uc = Ic / cw
jc = - p/2 }
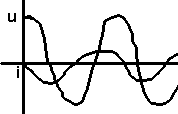
Récapitulatif
:
4)
Association des 3 dipôoles
Ex
: association en série RLC
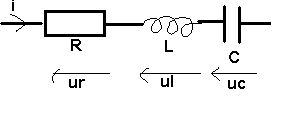
i
est la grandeur commune, on la prend comme origine des phases
i(t) = I sqr(2) cos
wt
ur(t) = R I sqr(2) cos wt
ul(t) = LwIsqr(2) cos (wt + p/2)
uc(t) = I / Cw sqr(2) cos (wt -
p/2)
2criture directe à partir du tableau récapitulatif
u = ur + ul + uc
= RIsqr(2) cos wt + LwI sqr(2) cos (wt+p/2) + I/Cw sqr(2) cos (wt-p/2)
en
avance de p/2 en
retard de p/2
sur
i donc sur ur sur
i donc sur ur
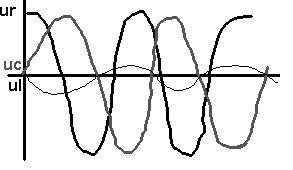
Si
on veut calculer u pour trouver U Ö2 cos (wt+j)
Source : www.fvirtman.fr.st
– Auteur : Fman
ÓSNOCLUB.fr.st