| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
I Régime forcé d'un circuit
Exemple
: circuit RLC
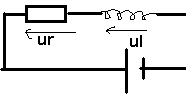
u(t) = u Ö2 cos wt
U
= Ur + Ul + Uc => dU/dt = dUr/dt + dUl/dt + dUc/dt
Ur
= RI
Ul
= L di/dt avec q = cUc <=> i = du/dt =
R di/dt + L di²/dt + i/c
di²/dt
+ R/L di/dt + i/LC = 1/L du/dt
i
= ip + ih
ih
vérifie l'équation différentielle en remplaçant le 2nd membre par 0
d²ih/dt
+ R/L dih/dt + ih/LC = 0 (Régime libre)
ih
= k1 er1t + k2 er2t
équation caractéristique
r²
+ R/L r + 1/LC = 0
D=R²/L² - 4/LC
-Si
D>0 :
r1 et r2 appartiennent à ![]() Régime apériodique
Régime apériodique
r1
= -R/2L + ½ ÖD }
r2
= - R/2L - ½ÖD } r1 et r2 sont toutes deux inférieures à
0
D< R²/L² } => t-> a => ih->0
-Si
D=0 r1=r2=-R/2L régime
critique
ih= (Dt + B)e-(R/2L)t
-> 0
t ->
a
-
Si D<0
régime pseudopériodique
D = - (4/LC
- R²/LC) } r1 et r2 appartient à C
= i²(4/LC - R²/L²)
}
ih = e(-R/2L)t (K1e(i/2)Öp + K2e(-i/2)Ö p)
| Dcos Ö(p/2) t + B sin Ö(p/2) t
t->a 0 K
cos ( Ö(p/2)t+q )
Pour
t suffisamment grand, ih->0, quelque soit R,L,C
i(t)-> ip régime permanent
ih constitue un régime transitoire
Le
second membre est de la forme 1/L du/dt <=> alternatif sinusoidal
de pulsation w, alors une solution particulière sera elle-même alternative
sinusoidale de même pulsation w
Régime
forcé
On
pourra donc écrire
i -> ip = I Ö2 cos (wt-j)
le
ut est de calculer U et I
La
méthode algébrique étant longue et compliquée, on va pour décrire l'état
électrique d'un réseau (valeur efficace des tensions et intensités, déphasage
entre eux)
Utilisation
:
- Méthode vectorielle = méthode de Fresnel
- Méthode symbolique = méthode complexe
II Méthode de Fresnel
g
= Y Ö2 cos (wt +q) -> Y> de module
YÖ2 tournant autour d'un point fixe O à la vitesse angulaire
w
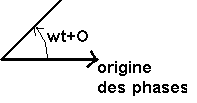
q est alors l'angle que fait Y> avec un axe origine
à t=0
si
y1 = Y1 Ö2 cos (wt + q1)
y2 = Y2 Ö2 cos (wt + q2)
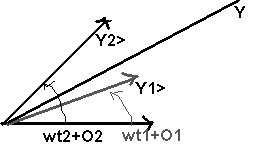
on
cherche y = y1 + y2 <=> Y>=Y1> + Y2>
je
mesure Y1Ö2 wt1 + q1
y= Y Ö2 cos (wt +q)
Simplification
:
-
Tous s verteurs tournent à la même vitesse angulaire, on peut effectuer
l'opération vectorielle à t=0
-
On peut également décider de prendre les valeurs efficaces et non les
amplitudes pour module
u = U Ö2 cos (wt +j)
u> = [UÖ2 ;j] ou u> = [U ;j]
i = I> Ö2 cos (wt -j) ;
I> = [ IÖ2 , -j ]
ou I> = [I, - j ]
2.2 Applications aux tensions et intensités
La
graphe de Fresnel va permettre d'additionner :
- des tensions entre elles (loi des mailles)
- des intensités ![]() (Loi des noeuds)
(Loi des noeuds)
Méthodologie
:
-
Se munir d'une règle graduée et d'un rapporteur
-
Si elle n'est pas imposée, choisir comme origine des phases la grandeur
commune (i en série, u en parallèle)
-
Déterminer les vecteurs associés aux grandeurs sinusoïdales (toutes en
valeurs efficaces ou toutes amplitudes)
-
Choisir une échelle commune aux grandeurs traitées (et s'y tenir)
Exemple
1 :
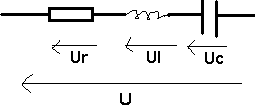
On
cherche u = ur + ul + uc sachant que :
Ur = 4 Ö2 cos wt ->
Ur> = [4 ; 0 ]
Ul = sqr(140) cos (wt + p/2) -> Ul> = [sqr(70) ; p/2 ] = [8,4 ; 90º]
Uc = 8 cos (wt - p/2) -> Uc>
= [4Ö2 ; - p/2 ] = [5,65 ;
-90º]
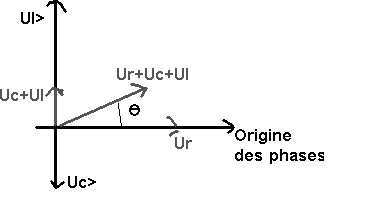
On
mesure :
U
= 4,8 V
q= 35 º
On
peut calculer :
U = sqr ( Ur² + (Ul - Uc)² )
Tan |q| = | Ul - Uc | / Ur
=> |q| = 34 º
U
en avance sur i => q = + 34º
U = 4.83 Ö2 cos (wt + 0.59 )
|-> q en radians
2ème
exemple
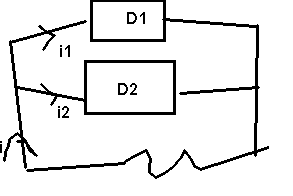
i1
a pour valeur efficace 6 A et un retard de 30º sur U
i2 a pour valeur efficace 2 A et un retard de 45 º sur U
On cherche i = i1 - i2 sachant que U = 220 Ö2
cos 100 pt avec U origine des phases
i1 = 6 Ö2 cos (100 p t - p/6) -> I1> = [6 ; -p/6]
régime forcé
i2 = 2 Ö2 cos (100 p t + p/4) -> I2> = [2 ; +p/4]
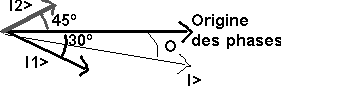
On
mesure : On calcule :
I = 6,7 A I>
= I1> + I2>
q= -14 º Ix = I1x +
I2x = I1 cos (-30º) + I2 cos (45º) = 6.61 A
Iy = I1y + I2y = I1 sin (-30º) + I2 sin (45º) = 1,58 A
I = sqr( Ix² + Iy² ) = 6,8 A
tangente
q = Iy / Ix
q= -13,5 º
i(t)
= 6,8 Ö2 cos (100 p t - ( 13,5 p )/ 180 )
LES VECTEURS NE SONT PAS COLINEAIRES
2.3 Applications aux dipôles élémentaires
u = U Ö2 cos wt -> i = I Ö2 cos (wt - phi)
U = I Ö2 cos (wt-phi)
-> i = Ö2 cos (wt)
f
= (I>,U>)
orienté
de i vers u
On
appelle impédance
d'une résistance
Zr = R
d'une bobine
Zl = L w
d'un condensateur
Zc =1 / c w
homogène à des ohms
2.4 Association de dipôles
Exemple
1 : Bobine réelle
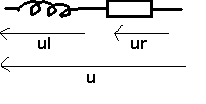
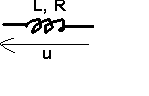
<=> i = I Ö2 cos wt ->
I = [ I; 0 ]
ul
-> Ul> = [LwI; + p/2]
ur
-> Ur> = [RI; 0 ]
u = ur + ul <-> U> = Ul>
+ Ur>
 Origine des j
Origine des j
Ul>
![]() Ur> => u = Ö( ur² + ul²)
Ur> => u = Ö( ur² + ul²)
u = Ö( R²I² + L²w²I²)
u
= Ö( R² + L²w²) I
Ö(R² + L²w²) = u/I = impédance du dipôle RL
tan
j = ul / ur = LwI / RI = Lw/R
u(t) = Ö(R² + L²w²) I Ö2 cos (wt + Arctan
Lw/R)
Exemple 2 : Condensateur réel
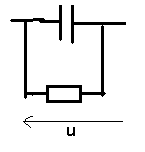
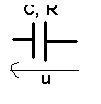
u = U Ö2 cos wt <-> u>
= [u,0]
ir
<-> Ir> = [ u/R, 0 ]
ic <-> Ic> = [Cw, + p/2 ]
i
= ic + ir <-> I> = Ic> + Ir>
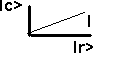 origine des j
origine des j
Ir>
+ Ic> => I = sqr( Ir² + Ic² ) = sqr( U²/R² + u²C²w²)
I
= Ö( 1/R² + C²w²) u
1
/ Ö( 1/R² + C²w²) = impédance du dipôle { R ![]() C }
C }
tan j = Ic / Ir = (u C w R)
/ u = R C w
i(t) = sqr( 1/R² + C²w²) u Ö2 cos (wt + arctan RCw)
j= (I>, u>)
= - arctan RCw dans i = I Ö2 cos (wt -j)
2.5 Limites de la méthode de Fresnel
Exemple
:
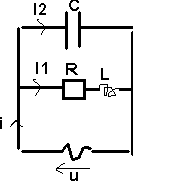
u
= 220 V
f = 50 Hz
R = 220 Ohm
L = 0.7 H -> Lw = L2pf = 220 Ohm
C = 7.25 µF -> 1 /Cw = 1/ C 2pf = 440 Ohm
On cherche i, i1 et i2
On
pose u, origine des j
<=> u = 220 Ö2 cos (100 p t) <-> u> =
[220,0]
i1 -> I1> = [ u/ (1/Cw) ; + p/2] = [220/400; + p/2] = [0.5; + p/2]
i2 > I2> = [u / sqr(R²+L²w²)
; - arctan ( Lw / R ) ]
= [ 200 / sqr(220² + 220²) ; -arctan 220/220]
= [1 /Ö2; - p/4 ] = [ 0.707; - p/4]
Graphe
à l'échelle :
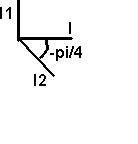
origine des phases (u>)
Ix = 0 + I2 cos (-45) = 1/Ö2 Ö2/2 = 0.5 A }
Iy = 0.5 + I2 sin(-45) = 0.5 - (Ö2/2)² = 0 A } =
=> I> = I1> + I2> = [0.5, 0 ]
||
i(t) = 0.5 Ö2 cos (100 p t)
Ur>
= [RI2; - p/4 ] <- en phase avec I2
Ul>
= [ LwI2; + p/4 ] <- en avance de p/2 sur I2
Ur + ul = U
Ur> + Ul> = U>
III - Méthode utilisant les
complexes
3.1 Principe général
Consiste
à associer à une grandeur sinusoïdale un vecteur dans le plan complexe
y
= Y Ö2 cos (wt +q) -> Y de module Y
ou YÖ2 faisant donc l'axe des réels (prix comme origine
des phases) <-> ![]() = Yeiq ou YÖ2eiq (avec
i² = -1)
= Yeiq ou YÖ2eiq (avec
i² = -1)
Rappel
: ![]() = a+ib = Yeiq = [ y , q]
= a+ib = Yeiq = [ y , q]
coor polaire Fresnel
![]() de {
y = module
de {
y = module
{ q = argument
Par
identification
a
= Re[y] = y cos q
b
= Im[y] = y sin q
y²
= a² + b²
cos
q = a / y sin q
= b/y
3.2 Application aux tensions et intensités
u = U Ö2 cos wt <--> u = u eiq = U
i = IÖ2 cos (wt -j) <-> ![]() = I e-ij
= I e-ij
= I cos j - i I sin j
ou bien
u = U Ö2 cos (wt +j) <-> u
= U eij= Ucos j + i U sin j
i = I Ö2 cos (wt) <->
![]() = I
= I
Application
:
*
Loi des noeuds
i = i1 + i2 <-> ![]() =
= ![]() 1 +
1 + ![]() 2
2
i1 = 2Ö2 cos (wt + p/4) <-> ![]() 1 = 2 ei p/4
1 = 2 ei p/4
i2 = 2Ö2 cos (wt + p/6) <-> ![]() 2 = 3e-ip/6 = 3
(Ö3/2 - i/2)
2 = 3e-ip/6 = 3
(Ö3/2 - i/2)
![]() = Ö2 + iÖ2 + 3 (sqr(3)/2
- i/2)
= Ö2 + iÖ2 + 3 (sqr(3)/2
- i/2)
= 4 -1,18 i
I
= 4,18 A
arg
I = Arctan - 1,18 / 4 = - 16,44º ou - 16,44 + 180
| ici car le
=> i(t) = 4,18 Ö2 cos(wt - (16,44
×p)/180 )
--------------------
0,28 radians
*
Loi des mailles
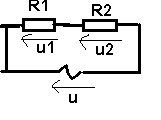 u2 ?
u2 ?
soit u = 220Ö2 cos wt
u1 = 50Ö2 cos (wt +p/3)
u= 220
u1= 50 eip/3= 50 (1/2 - iÖ3/2 )
u = u1 + u2 <=> u2 = u - u1 <--> u2=u-u1
u2 = 220 - (25 + 25 iÖ3 ) = 220 - 25 - 25 iÖ3= 195 - 25 iÖ3
u2 = Ö(195² + (25Ö3)² ) = 200 V
arg u2 = arctan -25 Ö3 / 195 = -12,5º = -
0,22 rad
=> u2(t) = 200 Ö2 cos (wt - 0,22)
3.2
U
/ I sont homogènes à des ohms, on appelle impédance complexe Z
Z= U / ![]() = Z eij =
2 cos j + i z sin j= R + i X
= Z eij =
2 cos j + i z sin j= R + i X
Re[Z]
= R = résistance du dipôle
R= Z cos
q
Im[Z]
= X = Réactance du dipôle
X
= Z sinq peut
être négative
Loi
d'ohm en alternatif => u = Z I
Pour
u origine des phases -> u = u
I = u / z = u / zeiq = (u / z) e-iq
I = u / z
arg I = - j = - arg z
Pour i origine des phases I = I
u = z I = z eiq I
u = ZI
arg u = +j = arg z

en
conclusion, on voit que dans z = z eiq
j= arg z = déphasage entre i et u à ses bornes
j= arg z = (I>,
u> )
3.4 Admittance d'un dipôle
On
définit l'admittance d'un dipôle complexe Y = 1 / z
z = zeiq => y = 1/z e-iq
->
y = 1/z
arg
y = -j = - arg z
z = R + iX
y = G + i H
G
= constance
H = susceptance
y = 1 / z =
1 / (R + iX) = 1 / (R + iX)
(R - iX) / (R-iX)
= (R - i X ) /
(R² + X² )= (R / (R² + X²) ) - i ( X / (R² + X²))
3.5 Application aux dipôles élémentaires
*
Résistance
Zr
= R
jr = 0
Zr = R
*
Bobine idéale
Zl
= Lw
jl = + p / 2
Zl = Lw eip/2 = iLw
*
Condensateur idéal
Zc = 1 / Cw
jc = - p / 2
Zc = 1 / C w e-ip/2 = - i / C w
Exmple
d'application :
Une
tension de 200 V (Ueff) , 50 Hz est appliquée à un circuit RLC série.
Déterminer l'intensité i sachant que R = 300, L = 300mH, C = 5 µF
1)
Calculer w=100p
2)
Caculer Lw = 95 Ohms 1 / Cw = 637 Ohms
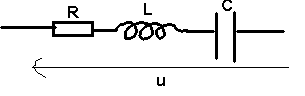
U = Z I
U = 200 (origine des phases)
Z = Zr + Zl +
Zc
= R + iLw + 1/ iCw
= R + i (Lw - 1/Cw)
= 300 + i(95 - 637) = 300
- 542i
arg Z = j = - 61 º
arg Z = arctang - 542 / 300
Z = sqr (300² + 542²)
= 620 Ohms
I = U / Z => I = U / Z = 200 / 620 = 0,32 A
arg I = arg U - arg Z
= 0 - j = + 61 º
= 61 p / 180 rad
i(t) = 0,32 Ö2cos (100pt + 61*p/180)
si demandé I = I cos j + I sin j
=
0,32 cos 61 + 0,32 sin 61
=
0,15 + 0,28i
3.6 Application générales de la méthode complexe
Toutes
les lois du continu sont applicables à condition de les utiliser sur les
grandeurs complexes
*
Lois de Kirchhoff
-
Loi des mailles : S = 0
-
Loi des noeuds : S I = 0
*
Loi d'association des impédances
-
série : ![]()
![]()
![]()
Z1 Zj Zn
Zeq
= S Zj
Zj = Rj + iXj
Re[Zeq] = Req = S Rj
-
parallèle : ![]() <=>
<=> ![]()
![]()
![]()
1
/ Zeq = S 1 / Zj <=> Yeq = S Yj
ATTENTION
: 1/Req différent de S 1/Rj
*
Théorème de superposition
*
Théorème de thévenin
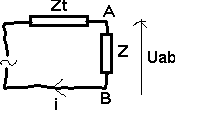
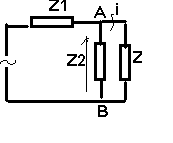 <=>
<=> 
Calcul
de ET
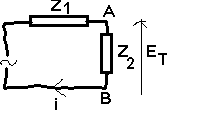
ET = Z1 U / Z1 + Z2
(division
de tension complexe)
Calcul
de ZT
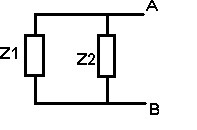
ZT = Z1 Z2 / Z1 + Z2
Alors
I = ET / ZT + Z
Loi de Pouillet en complexe
De
façon générale, si les expression instantanées des intensités ou tensions
ne sont pas demandés, l'état électrique d'un réseau sera considéré comme
complètement décrit par les modules et les arguments de ces intensités
ou tensions.
3.7 Méthodologie des nombres complexes
X1 = a1 + i b1 = q1 eio1
= q1 cos o1 + i q sin o1
X2 = a2 + i b2 = q2 eio2
= q2 cos o2 + i q sin o2
* Addition ou soustraction
X = X1 + X2 =
a1 + ib1 + a2 + ib2 = a1 + a2 + i(b1 + b2)
= a + ib
= q eio
a = a1 + a2
b = b1 + b2
=> q= sqr( (a1+a2)²
+ (b1+b2)² )
q= arg (b1+b2)/(a1+a2)
*
Multiplication (Forme polaire recommandée)
X = X1 X2
= (a1 + ib1)(a2 + ib2) =
a1a2 + b1b2 + i(a1b2 + a2b1)
= q1 eio2 2qeio2 = q1 q2 ei(o1+o2)
X = a + ib
= q eio
q = q1 q2
q = q1 + q2
a = q cos q = q1q2 cos(q1 + q2)
b = q sin q = q1q2 cos(q1 + q2)
q = Ö((a1a2 + b1b2)²
+ (a1b2 + a2b1)²)
q = arctan ( a1b2
+ a2b1 ) / (a1a2 - b1b2)
*
Division (forme polaire conseillée)
X = X1 / X2 = q1 eio1 / q2 eio2 = q1 / q2 ei(o1+o2)
X = a1 + ib1 / a2 + ib2 = ( a1a2 - b1b2 + i(b1a2 - a1b2) ) / ( a2² - b2²
)
X = a + ib
a = ( a1a2 - b1b2 ) / ( a2² - b2² )
b = ( b1a2 - a1b2 ) / ( a2² - b2² )
*
Elévation de la puissance (forme polair recommandée)
X = Xn = (q1n eino)
q = q1n
O
= nO
Ne
pas oublier
arg
nombre réel >0
= 0
<0 =
p
Arg
imaginaire >0 = + p/ 2
<0 = - p/ 2
Source : www.SNOCLUB.fr.st
– Auteur : Inc.
ÓSNOCLUB.fr.st