| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© SNOCLUB.fr.st
I
- Puissance instantanée, puissance active
1.1 Puissance instantanée
Dipole
:
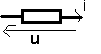
u = Ö2 cos wt
i = IÖ2cos (wt -j) (j= arg Z du dipôle)
A
l'instant t p(t) = u(t) i(t) = 2UI cos (wt -j)
p(t),
puissance instantanée, n'est pas accessible à la mesure
1.2 Puissance active
cos
p cos q = 1/2 [ cos (p+q) + cos(p-q) ]
p(t)
= 1/2 * 2UI [ cos (2wt -j) + cos j ]
p(t)
= UI cos j + UI cos (2w - j)
Terme constant Terme fluctuent
Calculons
la puissance moyenne mise en jeu pendant n périodes T
<p(t)>
= 1/ nT 0ònT
p(t) dt = 1/ nT 0ònT
UIcos j dt + 1/ nT 0ònT
UIcos (2w -j )dt
<p(t)>
= 1/nT UI cos 1/ nT cos j [t]nt0 + 1/nT UI [ sin (2wt
- j) / 2w ]
<p(t)>
= UI cos j + UI / nT2w [ sin (2wnT - j) + sin j ]
w
= 2p / T => 2wnT = 4pn
sin(4nT - j) = sin -j
On
appelle P = UI cos j (U et I sont les valeurs eficaces)
La
puissance active du dipole est le puissance effectivement dégagée par
le dipole (par effet joule dans les résistances du dipole)
Autre
expression de P = UI cos j
U = Z I
avec Z = Ze ij
Z = Z cos j + I Z sin j
U = ZI => P = ZI² cos j = Z cos j I²
Re[Z]
P = RI²
Attention
: P = ( U² / Z ) cos j
R =
Z cos j
P =
U² / R cos² j
II - Puissance complexe, réactive,
apparente
Par
homogénéité, on définit la puissance complexe
S = UI cos j + i UI sin j
S = UI eij
U = U
I = I e-ij
S = U ![]() (conjugué
de I)
(conjugué
de I)
ou
S = 1/2 U I
| si u = UÖ2 et I = IÖ2e-ij
2.2 Puissance réactive
On
appelle Q = UI sin j = puissance réactive ( elle existe mais n'est pas
effectivement dégagée )
Q
-> VAR ( Volt Ampère Réactif )
j appartient à [-p/2;
p/2]
Autre
expression de Q
U = ZI et Z = Z cos j + i Z sin j = R + i X
Q = ZI² sin j
Q
= XI²
| avec son signe
2.3 Puissance apparente
S
-> VA
Relations
entre ces puissances
S = P + i Q
S = sqr( P² + Q²)

2.4 Application aux dipoles élémentaires
| Dipole | P = UI cos j | Q = UI sin j |
| Résistance Z=R j=0 |
P = U I = R I² = Ur² / R |
0 |
| Bobine Z=Lw j=p/2 |
0 | Q = U I = Lwi² = Ul² / Lw |
| Condensateur Z=1/Cw j=-p/2 |
0 | Q = - Uc Ic = - Ic² / Cw = -Cw Uc² |
2.5 Théorème de Boucherot
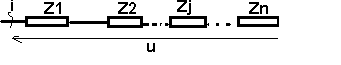
S = U Ib si { U
= [ U , 0 ] et I = [ I , -j ]
{ ou
U = [ U, j ] et I = [ I
, 0 ]
ou
bien
Loi
des mailles :
U = S (j=1 à n) Uj
I = S (j=1 à n) Sj P = S (j=1 à n) Pj Q = S
(j=1 à n ) Qj
Attention
: somme algébrique : avec leur signe
Sj = Pj + i Qj
S = P + iQ
Le
raisonnement se réitérant pour 1 circuit parallèle ( en utilisant la loi
des noeuds en complexes), on peut énoncer le théorème de Boucherot.
-
La puissance active d'un réseau est égale à la somme des puissances actives
consommées par chaque dipole du réseau
-
Idem pour la puissance réactive (somme algébrique)
Zj = Rj iXj
traversé par Ij
Pj = Rj Ij²
Qj = Xj Ij²
D'où
l'autre forme du théorème de Boucherot :
P
= S (j=1 à n)
Pj = S (j=1 à n) Rj Ij²
Q
= S (j=1 à n)
Qj = S (j=1 à n) Xj Ij²
Exemple
:
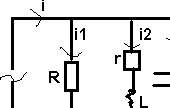
Calcul
de P et Q
1ère
méthode par P= U I cos j
Q = U I sin j
On
calcule Zeq = Z eij
I = U / Z
2ème
méthode : Boucherot
On
calcule toutes les intensités (valeurs efficaces)
P = RI1 + rI2 } = UI cos j
Q = ( L w I2² ) - ( I3² / C w ) }
= UI sin j
III - Facteur de puissance
3.1 Définition
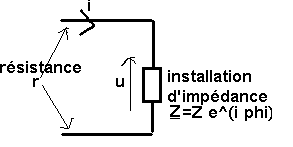
P
= U I cos j effectivement
dégagée
I = P / (U cos j)
On
appelle k = cos j = facteur de puissance
Donc
pour une puissance facturée et une tension imposée, l'intensité I en ligne
varie avec 1 / cos j
Les pertes Joules dans les lignes d'arrivée d'alimentation de résistance
r s'élèvent à RI² pour EDF
Pour diminuer ces pertes Joules,
EDF peut alors :
- diminuer r en augmentant le diamètre des fils (mais s'en
suit un surcout)
- augmenter U (problème
de transport de hautes - tensions)
- augmenter cos j
EDF
impose donc aux usines un cos j (facteur de puissance) au moins égal à 0.8 seuil
en-deça duquel ils facturent des pénalités.
3.2 Relévement du facteur de puissance
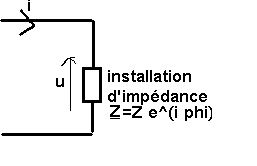
Installation
= beaucoup de moteurs => Bobinage => j > 0

Pour
remonter le cos j (diminuer l'angle j),
on monte des condensateurs en parallèle sur l'installation
Problème
: Quelle capacité C à monter en parallèle pour remonter cos j à cos j' > cos j
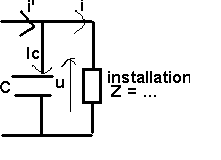
intensité
de l'installation inchangée
Dans
l'alimentation : i -> i' = i + ic
1ère
méthode : Par Fresnel
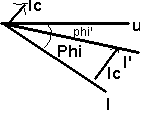
I'> = I> + Ic>
Ic>
est en avance de p/2 sur u>
Ic = I sin j - I' sin j
I = U C w
C = ( I sin j - I' sin j )/ U w
2ème
méthode : par Boucherot
| Avant la pose du condensateur | Après la pose du condensateur |
| P = UI cos j | P'= U I' cos j' = P + (Pc) |
| Q = UI sin j ( > 0 ) | P' = U I cos j |
| => I' = (I cos j )/ cos j' |
|
| Q' = UI' sin j' = Q + Qc | |
| Q' = UI sin j + Qc | |
| Qc = - Cw U² | |
| => Qc = UI' sin j' - UI sin j = -Cwu² | |
| C = ( I sin j = I' sin j' )/ uw | |
| ou bien Qc = Q' - Q | |
| Qc = P' tan j' - P tan j | |
| P = P' Qc = cwu² | |
| C = P(tan j - P' tan j') / u² w |
IV - Adaptation d'impédances
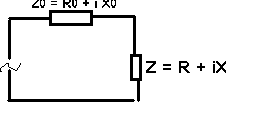
On
cherche Z (c'est à dire R et X) pour que la puissance dissipée
dans Z soit maximale
P = R I²
I = U / Z0 + Z
I = u / ( R0 + R + i(X0 + X) )
=> I = u / Ö( (R0+R)² + (X0+X)²
)
P = RU² / ((R0+R)² + (X0+ X)²)
P
= f(R,X)
P
est maximale pour ( a P / a X )R = 0
(a P / a
R )X =0
(a P / a X)R = ( RU² 2(X+X0) ) / [ (R+R0)² + (X+X0)²
]² = 0
=> X = X0
=> P = RU² / (R+R0)²
=> d P / d R = ( (R+R0)² - 2R(R+R0) ) / (R+R0)4
d P / d R =( (R+R0 - 2R) / (R+R0)³ ) U²
= ( (R0-R) / (R+R0)³ )U = 0 (pour R=R0)
Concusion
: La puissance dissipée dans Z est maximale quand
Z = R0 - i X0 = Z0
Alors
Pmax = U² / 4 R0²
Source : www.SNOCLUB.fr.st
– Auteur : Inc.
ÓSNOCLUB.fr.st