| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© SNOCLUB.fr.sts
On a vu que des réseaux comportant bobines et/ou condensateurs ont des
impédances qui sont dépendante de la fréquence
Z
= U / I
Donc
à U fixé, I = f(w)
à
I fixé, U = f(w)
On
s'intéresse à présent à la réponse en fréquence de U ou de I
I - Réponse d'un circuit R,L
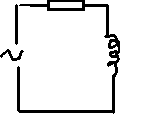
Ur = R U / R + iLw
->
Ar = Ur / U (coefficient
d'atténuation ou gain aux bornes de la résistance)
Ar = R / R + iLw
Ar
= R / Ö( R² + L²w² )
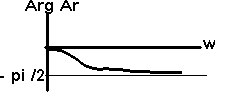
arc
Ar = 0 - arctan Lw / R
arc
Ar = déphasage entre Ur et U
= - arctan Lw
/ R
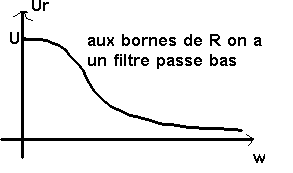
Ul = iLw U / R + iLw
Al = iLw / R + iLw
-> Al = Lw / sqr(R² + L²w²)
arg Al = + p/2 - arctg Lw / R

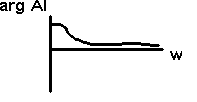
Pour
tout w
Ur + Ul = U
<=>
Ar + Al = 1
II - Réponse en fréquence d'un
circuit RLC série à U fixé
1) Comportement de l'impédance (Z)
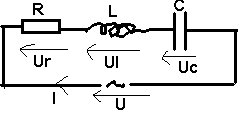
Z = R + iLw -i / cw
Z = Ö( R² + (L w - 1/cw)² )
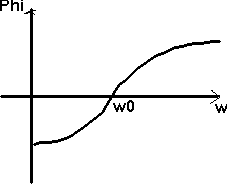
arg Z = j = I>, U>
= arctan ( (Lw
- 1/cw ) / R)
Quand :
w
-> 0, Z-> a
et arg
Z -> - p / 2
w
-> a,
Z -> a
et arg
Z -> + p / 2
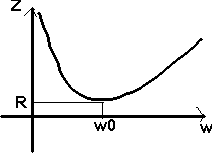
Z
est minimale pour Lw - 1/cw = 0
<=>
w = w0 = 1/ÖLc pulsation
propre
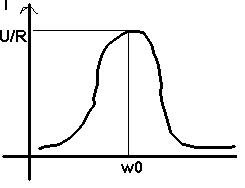
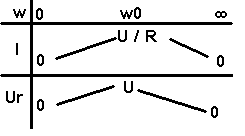
I = U / Z
I
= U / Z à U fixé, I passe par un maximum (U/R) pour w=w0
Il
y a résonance d'intensité
Remarque
: à I fixé, U passe par un minimum pour w=w0. C'est l'anti-résonance
2) Réponse aux bornes de R
Ur = RU / Z
-> Ur = RU / Z
= RU / Ö(R² + (Lw-1/cw)²)
= R I
P
= RI² = Ur² / R
P
est maximale pour w=w0. Alors Pmax = U² / R
Inversemment,
on a atténuation pour P < Pmax / 2
On
définit 10 log P exprimé en décibels (dB).
On
cherche le domaine de fréquence pour lequel la puissance aux bornes de
la résistance supérieur à Pmax / 2
10
log P >= 10 log Pmax - 10 log 2
= 0.3
On
cherche donc l'atténuation à - 3 dB
10 log Ur² / R >= 10 log U²/R - 3
<=> 20 log Ur - 10 log R >= 20 log U - 10 log R - 3
<=> 20 log Ur >= 20 log U
- 3
P >= Pmax / 2 <=> Ur² / R >= U² / 2R
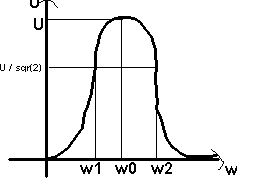
Dw = w2 -
w1
= bande passante
et
w1 et w1 sont les pulsations de coupure à -3 dB
On
pose x = w / w0 (on cherche donc x1 = w1 / w0
et x2 = w2 / w0 )
On
définit Q = Lw0 / R
= 1
/ RCw0
= facteur
de qualité (ou de surtension)
On
calcule w1 et w2 par les valeurs positives tirées de
(Lw / R - 1 / Rcw)² = 1
(
Qx - Q / x)² = 1 <=>
(x - 1/x)² = 1/Q²
=> x - 1/x = ± 1/ Q
= e
/ Q (avec e = ± 1)
x²
+ ex / Q - 1 = 0
D = e² / Q² + 4
= 1 / Q² + 4
x1,2
= - e / Q ± Ö(D/ 2 )
*
e = + 1 x1 = - 1 / 2Q + Ö( (1 / 4Q²) + 1) = w1 / w0
*
e = - 1 x2 = 1 / 2Q + Ö( (1/ 4 Q²) + 1) = w2 / w0
Dw = w1 – w2 = w0 / Q
Plus
Q est élevé, plus le circuit est sélectif
Aux
bornes de R on a donc un filtre passe bande
3) Réponse aux bornes de C
Uc = ( Zc U )/ Z
= U / ( icw [ R + i (Lw -
1/cw) ] )
= U / ( iRcw + 1 - Lcw² )
Uc = U / sqr( (1 - Lcw² )² + R²L²w² )
w->0 Uc ->U
w
= w0 Uc -> Q
U
w
-> + a Uc -> 0
On
étudie Uc = f(w)
Uc = U / sqr((1- w² / w0²)² + (w²
/ Q²w0²) )
= U / sqr ( (1 - x²)² + x²/Q²
)
Calcul
de d Uc / dx
= (- U / 2) ( [ 2(1 - x²)(-2x) + 2x
/ Q² ] / [ (1-x²)² + x² / Q² ]3/2
=
- Ux ( 1/Q² - 2 + 2x²) / [......]3/2
D
Uc / dx = 0 pour x = 0
pour x² = 1 - (1 / 2Q²) si 1 - (1/ 2Q²) > 0
<=>
1 / 2Q² < 1
<=> Q > 1 / Ö2
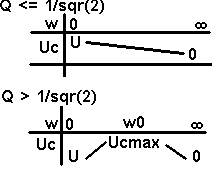
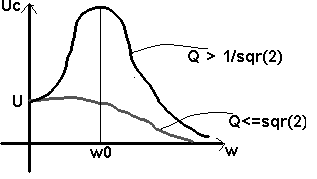
Pour
Q >> 1
Ucmax
pour w » w0
Alors
Ucmax = QU
| facteur de surtension
On
retrouverait le même type de phénomène aux bornes de L
En
particulier, à la résonance (w = w0 et quand Q>>0)
Ur = U = Ul + Uc = 0
On
aura donc également surtension de QU aux bornes de L (déphasé de p
par rapport à Uc)
III - Conclusion
Les
composants RLC sont utilisés pour filtrer des fréquences.
Il
existe des filtres :
- Passe bas : aux bornes de R laisse passer les fréquences de 0 à f0 =
2p/w0
-
Passe haut : aux bornes de R laisse passer les fréquence de f0 = 2p/w0 à a
* Retour sur RL : Ur/U = R / Ö(R²
+ L²w²) Ul/U = Lw / Ö( r² + L²w²)
Les valeurs max Ur = Ul = U
La pulsation de coupure
à - 3 dB s'obtient pas Ur = Umax / Ö2
Pour Ur = U / Ö( 1 + L²w² / R²)
pour 1 + L²w² / R²=2
Pour Ul = U / Ö( 1 + R² / L²w²)
=> w² = R² / L² = w0²
-
Passe bande
-
Coupe bande (ou réjecteur de fréquence)
ÓSNOCLUB.fr.st