| Biologie | Chimie | Informatique |
| Math | NTIC | Physique |
|
|||||
| Communauté | |
| Cours | |
| Emploi | |
| Logement | |
| Universités | |
| Réforme "LMD" | |
| Services | |
| Jeux | |
| Info | |
| Météo | |
| Plus | |
| Accueil | |
| Liens |
Le site n'est plus mis a jour actuellement...
© SNOCLUB.fr.st
I] Introduction
1) Rappels
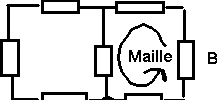
Réseau électrique : ensemble de dipoles reliés entre eux par un conducteur de résistance négligeable
- Réseau actif : lorsque le réseau contient des dipoles actifs (générateurs), c'est un réseau qui fournit de l'énergie et dont la caractéristique ne passe pas par l'origine.
- Réseau passif : c'est un réseau qui ne contient pas de générateur, il va consommer l'énergie et sa caractéristique passe par l'origine.
2) Problématique
On s'intéresse aux réseaux électriques contenant des dipoles actifs ou passif linéraires et en régime continu. On va donc établir des lois ou des théorèmes permettant la résolution de ces réseaux
II]
Groupement d'éléments passifs
1) Association de résistances en série
Si on considère une portion AB d'un circuit contenant des résistances, l'enseble de cette portion de circuit étant parcouru par une intensité I
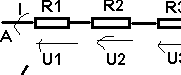
U
= U1 + U2 + U3 = R1I + R2I + R3I
U = (R1 + R2 + R3) I
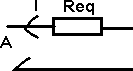
U = Req I
Req
= iEsomme Ri
2) Association de résistances en parallèle
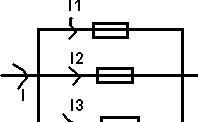
I
= U/R1 + U/R2 + U/R3
= U (1/R1 + 1/R2 + 1/R3)
I = U / R
1/ Req = iEsomme 1/Ri
Geq = iEsomme Gi
G = conductance (inverse de la résistance)
3) Montage diviseur de tension
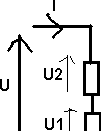
U1
= f(U,R1,R2)
U
= (R1+R2)I
U1
= R1I => I = U1 / R1
U
= (R1+ R2 ) (U1/R1)
U1
= ( R1 / ( R1+R2 ) ) U
4) Montage diviseur de
courant
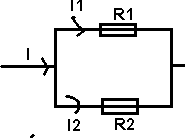
I1
= f(I1,R1,R2)
I
= I1 + I2
U
= R1 I1 = R2 I2 => I2 = R1/R2
I1
I
= I1 + R1/R2 I1
I
= (1 + R1/R2) I1
I1 = R2 / (R1 + R2) I Relation diviseur de courant
1/
Req = 1/R1 + 1/R2
=> Req = R1 R2 / (R1+R2)
U
= ReqI = R1I1
I1
= (Req I ) / R1
III]
Les lois de Kirchhoff
1) Enoncé des lois
* Loi des noeuds : elle exprime que la somme algébrique des courants qui arrivent à un noeud est égale à la somme algébrique des courants qui en sorte.
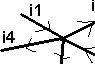
I1
+ I2 = I3 + I4 + I5
convention
: on fait précéder du signe plus les courants qui arrivent sur le noeud
et du signe moins les courants qui en sorte
kEsomme
±Ik = 0
2) Loi des mailles
La
loi des mailles traduit le fait que sur un maille, la somme des tensions
est nulle. Ayant choisi sur une maille un sens de parcourt arbitraire,
on écrit que sur cette maille, jEsomme ± Uj = 0
Les conventions :
- Si le sens de parcourt est dans le même sens que la tension, c'est plus, sinon c'est moins.
jEsomme
Rj Ij = jEsomme
Ej
Régles d'utilisation :
- On choisi arbitrairement le sens des courants dans les différentes branches
- On choisi sur la maille un sens de parcourt arbitraire
- Le produit RI est précédé du signe plus lorsque le sens de parcourt de la maille coincide avec le sens arbitraire de circulation du courant dans la branche
-
Le terme E est précédé du signe de la borne par laquelle on sort en suivant
le sens de parcourt de la maille.
3) Exemples d'application
Exemple
1 :
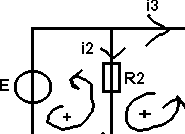
2
noeuds
3 branches3
mailles => seules 2 mailles sont indépendantes
Loi
des noeuds : I1 = I2 + I3
2) R2I2 - R3I3 = 0
{
I1 = I2 + I3
{ R1 I1 + R2 I2 = E
{ R2 I2 - R3 I3 = 0
(3)
I3 = (R2 / R3) I2
(1)
I1 = I2 + (R2/R3)I2
I1 = I2 ( 1 + R2/R3 )
(2) R1 ( 1 + R2/R3)I2 + R2I2 = E
I2 { R1 ((R2 + R3) / R3) + R2 }
= E
I2 { ( R1R2 + R1R3 + R2R3 ) / R3
} = E
I2 = E R3 / ( R1R2 + R2R3 + R1R3
)
I3 = +E R2 / ( R1R2 + R1R3 + R2R3
)
I1 = E(R2 + R3) / ( R1R2 + R1R3
+ R2R3 )
*
Exemple 2
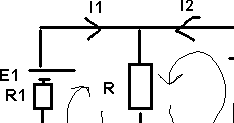
R1
= 1 Ohm
R2 = 2 Ohm
R = 10 Ohm
E1 = 6 V
E2 = 12 V
Loi
des noeuds
(1) I3 = I1 + I2
Loi des mailles
(2) r1I1 + RI3 = E1
(3) RI3 + r2I2 = E2
(2)
<=> I1 = (E1 - RI3 ) / r1
(3)
<=> I2 = (E2 - RI3 ) / r2
(1)
<=> I3 = (E1 - RI3) / r1 +
(E2 - RI3) / r2
I3
( 1 + R/ r1 + R / r2 ) = E1 / r1 +
E2 / r2
I3
( (r1r2 + r2R + r1R ) / r1r2 = E1E2 + E2E1 / r1r2
I3
= (r2E1 + r1E2) / (r1r2 + Rr1 + Rr2)
I3
= 0.75 A
I1
= - 1.5 A
I2 = 2.25 A
I1 circule donc dans le sens opposé que celui choisi arbitrairement
IV]
Théorème de superposition
1) Enoncé du théorème
La
tension entre deux points A et B d'un circuit électrique linéaire comportant
plusieurs générateurs est égale à la somme des tensions entre ces deux
points lorsque chaque générateur agit seul, les autres étant remplacés
par leur résistance interne. De même, l'intensité dans une branche AB
d'un circuit électrique linéaire est égale à la somme des intensités dans
cette branche lorsque chaque générateur agit seul.
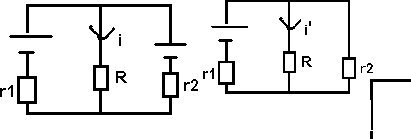
2) Exemple d'application
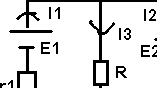
1ere étape : On laisse E1 allumé et on enlève E2
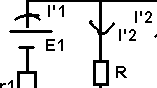
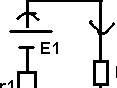
Req = Rr2 / R1 + R2
r1I'1 + ReqI'1 = E1
I'1
= E1 / (r1 + (Rr2 / R + r2))
I'1
= (R+r2)E1 / (r1R + Rr2 + r1r2)
I'1
= 2,25 A
U
= RI'3 = E1 - r1I'1
I'3
= E1/R - (r1/R) I1
I'3
= 0.375 A
I'2
= (R/r2) I'3
I'2
= -1.875 A
2eme
étape :
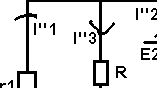
I"2
= E2 / ( r2 + (r1R / r1+R) )
I"2
= (r1 +R) E2 / ( r1r2 + r1R + r2R )
I"2
= 4,125 A
U
= - r1I"1 = RI"3 = E2 - r2I2
{
I"3 = E2/R - (r2/R)I"2
{
I"1 = - E2/r1 + (r2/ri) I"2
=> I"1 = - 3,75 A
I1
= I'1 + I"1 = - 1.5 A
I2
= I'2 + I"2 = 2.25 A
I3
= I'3 + I"3 = 0.75 A
V]
Thèorème de thévenin
1) Enoncé de Thévenin
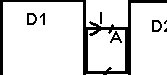
D1 est un ensemble de dipoles contennant des générateurs
D2
est un ensemble de dipoles ne contennant pas de générateurs
Enoncé du théorème : Toute portion de circuit ne comportant que des dipoles actifs et passifs linéaires peut être remplacée par un dipole actif linéaire appelé générateur de thévenin.
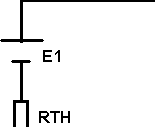
Soient deux dipoles d1 et d2 ayant en commun la tension Uab et le courant I. On peut remplacer d1 par un modèle équivalent de thévenin dont la caractéristique est donnée par Uab = ETH - RTHI
ETH est la force électromotrice de thévenin et RTH sa résistance interne.
Lorsqu'on
coupe la liaison entre les deux dipoles d1 et d2, on a aux birnes de d1
une intensité nulle et la tension Uab est égale à ETH ETH représente la tension à vide
aux bornes de d1. La résistance de thévenin RTH est la résistance
équivalente entre A et B lorsque tous les générateurs du dipole d1 sont
éteints
- ETH

- RTH
RTH
= Résistance équivalente
de D1 lorsque les générateurs sont éteints
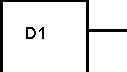
2) Exemple d'application
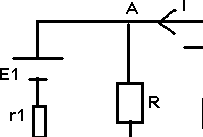
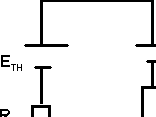
ETH
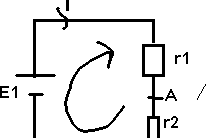
I = E1 / (r1 + R)
ETH
= RI = RE1 / (r1 + R)
2ème
étape : RTH (résistance lorsque les générateurs sont éteints)
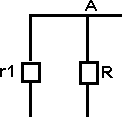
RTH
= RAB = r1R / (r1 + R)
ETH
= RE2 / (r1 + R)
rI2
+ RTH +I2 = E2 - ETH
I2
= (E2 - ETH )/ ( r1 + RTH )
I2
= ( E2 - (RE1 / r1 + R) ) / ( r2 + (r1R / r1 + R) )
I2
= E2(r1+R) - RE1 / r1r2 + r1R + r2R
I2
= 2.25 A
VI]
Transformation Triangle-Etoile (de Kennelly)
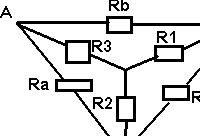
R3 = RaRb / (Ra+Rb+Rc)
R2 = RaRc / (Ra+Rb+Rc)
R1
= RbRc / (Ra+Rb+Rc)
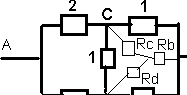
Rab
?
Rc
= 1*1 / 4 = 0.25 Ohms
Rb
= 1*2 / 4 = 0.5 Ohms
Ra
= 1*2 / 4 = 0.5 Ohms
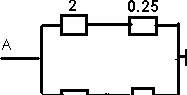
Rab = 0.5 + (9/4 * 3/2) / (9/4 + 3/2)
Rab
= 1.4 Ohms
Source : www.SNOCLUB.fr.st
– Auteur : Inc.
ÓSNOCLUB.fr.st